Covid-19: Fighting a fire with water or gasoline? Whispers from the 1930s

I’ve been reflecting a bit on the global Covid-19 situation for the last couple of weeks, and I fear government failures around the world. The world governments’ reaction to the novel Coronavirus risks pushing our economies into a deep global recession. There is often an enormous cost to “an abundance of caution”. Are the risks worth the trade-offs?

Covid-19: Ground zero of a global recession?

The recent statement last week by the World Health Organization, claiming that 3.4% of those who caught Covid-19 died, is in all likelihood a gross upward bias of the true mortality rate. In South Korea, a country that has been hit particularly hard by the infection, the authorities there have administered more than 1,100 tests per million citizens. Analysis of their data suggests a mortality rate of 0.6%. As a point of comparison, the seasonal flu has a mortality rate of about 0.1%. High mortality from early estimates of Covid-19 seem to result from extreme truncation – a statistical problem that is not easy to solve. People who present themselves at medical facilities tend to be the worst affected making observation of those individuals trivial, while those who have mild symptoms are never heard from. Covid-19 is probably more dangerous than the flu for the elderly and those with pre-existing conditions which is almost certainly the main driver of the higher mortality rate relative to the seasonal flu. Italy’s numbers seem to be an outlier, but it’s unclear exactly what testing strategy they are using. At any rate, what worries me is not Covid-19 but the seemingly chaotic, on-the-fly world government responses that threaten to turn a bad but manageable problem into a global catastrophe. We have a precedent for such government policy failures in the past: The Great Depression.

In the late 1920s, in an attempt to limit speculation in securities markets, the Federal Reserve increased interest rates. This policy had the effect of slowing economic activity to the point that by August of 1929 the US economy fell into recession. Through gold standard channel mechanisms the Federal Reserve’s policy induced recessions in countries around the world. In October the stock market crashed. By itself, even these poor policy choices should not have caused a depression, but the Federal Reserve compounded its mistakes by adopting a policy of monetary contraction. By 1933 the stock of money fell by over a third. Since people wished to hold more money than the Federal Reserve supplied, people hoarded money and consumed less, choking the economy. Prices fell. Unemployment soared. The Federal Reserve, based on erroneous policy and on further misdiagnoses of the economic situation, turned a garden variety but larger than average recession into a global catastrophe. The former chairman of the Federal Reserve Ben Bernanke, and an expert on the Great Depression, says:

“Let me end my talk by abusing slightly my status as an official representative of the Federal Reserve. I would like to say to Milton [Friedman] and Anna [Schwartz]: Regarding the Great Depression, you’re right. We did it. We’re very sorry. But thanks to you, we won’t do it again.”

Unintentionally, the Federal Reserve’s poor decision making created a global disaster. This is the face of government failure. Poor polices can lead to terrible consequences that last decades and scar an entire generation.

When an entire economy largely shuts down by government fiat for a few weeks or a month, it is not as simple as reopening for business and making back the losses when the crisis passes. During the shutdown, long term contracts still need to get paid, employees still need to get paid, business loans still need to get repaid, taxes are still owed, etc. When everything restarts, businesses are in a hole so it’s not back to business as usual. Some businesses will fail; they will never catch up. Some people will accordingly lose their jobs. Production and supply chains will need to adjust; an economic contraction becomes likely. Quickly shutting down an economy is a bit like quickly shutting down a nuclear reactor: you must be really careful or you risk a meltdown. With Covid-19 policies, governments around the world are risking the economic equivalent. The stock market is rationally trying to price the probability of a policy-induced catastrophe, hence the incredible declines and massive volatility.

Every day 150,000 people die on this planet. How much do we expect that number to change as the result of Covid-19? Are polices that risk a serious global recession or worse worth it? Maybe. But that’s a serious set of consequences to consider. Maybe we will get lucky and we will largely escape unscathed and it will all pass soon. Or maybe not. Yet a comparison to the Federal Reserve’s policy actions in the late 1920s and early 1930s generates an unsettling feeling of deja vu: Made-on-the-fly world government responses, rooted in an “abundance of caution” with more than a touch of panic, is putting the world economy on the cusp of a global catastrophe.

The depth of a serious government failure is beyond measure. It’s not climate change that’s the biggest threat to humanity; it’s unforeseen events coupled with risky policy responses, like the situation we currently find ourselves in, that should really worry us. Real problems come out of nowhere, just like Covid-19, not stuff that might happen over a hundred years with plenty of time to adapt. Let’s all demand careful policy responses and weigh the risks and consequences appropriately. Otherwise, we just might find out how true the aphorism is:

History might not repeat itself, but it does rhyme.

UPDATE – March 13, 2020

Policy choices have trade-offs. When policy is slapped together in a panic more often than not the hastily constructed policy produces little value in solving the problem but creates enormous secondary problems that eclipse the original problem’s severity. We need to be careful. It doesn’t mean we ignore the problem, over course saving lives matter and we should all do our part to help. But swinging post-to-post with large policy shifts that appear faster than the 24 hour news cycle, as we have seen in some countries, is a very risky policy response. We don’t want to do more harm than good. Fortunately, it appears that governments around the world are beginning to have more coordinated conversations.

More than anything, I think this experience points to the need for serious government and economic pandemic plans for the future. It’s a bit ironic that policy has started to demand stress testing the financial system for slow moving climate change effects, but no one seemed to include pandemics. How many financial stress tests evaluated the impact of what’s happening right now? This event is a wake up call for leadership around the world to be more creative in thinking about what tail events really look like. Having better plans and better in-the-can policy will protect more lives while preserving our economic prosperity.

Finally, a serious global recession or worse is not something to take lightly. Few of us have experienced a serious economic contraction. If the global economy backslides to a significant extent, the opportunities we have to lift billions of people out of poverty gets pushed into the future. That costs lives too. Economic growth is a powerful poverty crushing machine. Zoonotic viruses like Covid-19 almost always result from people living in close proximity to livestock, a condition usually linked to poverty. In a world as affluent as Canada, the chance of outbreaks like the one we are witnessing drop dramatically. I hope that the entire world will one day enjoy Canada’s level of prosperity.

A paper to read by Gelman and Shalizi: Philosophy and the practice of Bayesian statistics

The great 20th century physicist Richard Feynman supposedly quipped “Philosophy of science is about as useful to scientists as ornithology is to birds.” As always, Feynman has a point, but in the fields of statistics, machine learning, and data science, understanding at least some of the philosophy behind techniques can prevent an awful lot of silliness and generate better results.

Feynman: You philosophers!

In their paper, Philosophy and the practice of Bayesian statistics, (British Journal of Mathematical and Statistical Psychology 2013, 66, 8-38) Andrew Gelman and Cosma Shalizi offer a thoughtful piece on what is really going on – or what really should be going on – in Bayesian inference. This paper is a short, highly interesting read, and I strongly suggest that all data scientists in the federal government put it on their reading lists.

For the uninitiated, statistical inference falls into two broad schools. The first, often called “classical statistics”, follows Neyman-Pearson hypothesis tests, Neyman’s confidence intervals, and Fisher’s p-values. Statistical inference rests on maximizing the likelihood function, leading to parameter estimates with standard errors. This school of statistics is usually the first one people encounter in introductory courses. The second school – Bayesian statistical inference – starts with a prior distribution over the parameter space and uses data to transform the prior into a posterior distribution. The philosophies behind each school are often said to be deductive in the classical case, and inductive in the Bayesian one. The classical school follows a method that leads to rejection or falsification of a hypothesis while the Bayesian school follows an inductive “learning” procedure with beliefs that rise and fall with posterior probabilities. Basically, if it’s not in the posterior, the Bayesian says it’s irrelevant. The Bayesian philosophy has always made me feel a bit uncomfortable. Bayesian methods are not the issue, I use them all the time, it’s the interpretation of pure inductive learning that has always bothered me. To me, I’ve felt that in the end the the prior-to-posterior procedure is actually a form of deductive reasoning but with regularization over the model space.

Gelman and Shalizi go right to the heart of this issue claiming that “this received view [pure inductive learning] of Bayesian inference is wrong.” In particular, the authors address the question: What if the “true” model does not belong to any prior or collection of priors, which is always the case in the social sciences? In operations research and anything connected to the social sciences, all models are false; we always start with an approximation that we ultimately know is wrong, but useful. Gelman and Shalizi provide a wonderful discussion about what happens with Bayesian inference in which the “true” model does not form part of the prior, a situation they label as the “Bayesian principal-agent problem”.

In the end, Gelman and Shalizi emphasize the need for model testing and checking, through new data or simulations. They demand that practical statisticians interrogate their models, pushing them to the breaking point and discovering what ingredients can make the models stronger. We need to carefully examine how typical or extreme our data are relative to what our models predict. The authors highlight the need for graphical and visual checks in comparisons of the data to simulations. This model checking step applies equally to Bayesian model building and thus in that sense both schools of statistics are hypothetico-deductive in their reasoning. In fact, the real power behind Bayesian inference lies in its deductive ability over lots of inferences. The authors essentially advocate the model building approach of George Box and hold to a largely Popperian philosophy.

Finally, Gelman and Shalizi caution us that viewing Bayesian statistics as subjective inductive inference can lead us to complacency in picking and averaging over models rather than trying to break our models and push them to the limit.

While Feynman might have disparaged the philosopher, he was a bit of a philosopher himself from time to time. In an address to the Caltech YMCA Lunch Forum on May 2, 1956, he said:

“That is, if we investigate further, we find that the statements of science are not of what is true and what is not true, but statements of what is known to different degrees of certainty: “It is very much more likely that so and so is true than that it is not true;” or “such and such is almost certain but there is still a little bit of doubt;” or – at the other extreme – “well, we really don’t know.” Every one of the concepts of science is on a scale graduated somewhere between, but at neither end of, absolute falsity or absolute truth.

It is necessary, I believe, to accept this idea, not only for science, but also for other things; it is of great value to acknowledge ignorance. It is a fact that when we make decisions in our life we don’t necessarily know that we are making them correctly; we only think that we are doing the best we can – and that is what we should do.”

I think Feynman would have been very much in favour of Gelman’s and Shalizi’s approach – how else can we learn from our mistakes?

What does it take to be a successful data scientist in government?

Oh, no…yet another blog post on what it takes to be successful (fill in the blank). What a way to start 2020!

But, last month I was conducting job interviews and at the end of one interview the candidate asked me this very question. So, I thought I would share my answer.

There is endless hype about data science, especially in government circles: AI/deep learning will solve everything – including climate change – chatbots are the future of “human” service interaction, etc. Yes, all of these methods are useful and have their place, but when you ask the enthusiastic official jumping up and down about AI exactly which problem he hopes to solve and how he thinks AI or deep learning applies, you get a muddleheaded response. Most of the problems people have in mind don’t require any of these techniques. Unfortunately, in the rise toward the peak of inflated expectations, people often promote “solutions” in search of problems instead of the other way around.

My zeroth rule to becoming a successful data scientist: Avoid the hype and instead concentrate on building your craft. Read. Code. Calculate.

Data science applied in government requires three pillars of expertise: mathematics and statistics, hard coding skills, and a thorough contextual understanding of operations.

Mathematics and Statistics

With the explosion of data science there are, to be frank, a lot of counterfeits. Expertise is not something that can be built in a day, in a couple months, or through a few of online courses – it takes years of dedication and hard work. Data science in government and most business operations is not about loading data into black boxes and checking summary statistics. To make better decisions, we almost always seek a causal understanding of the world, generating the ability to answer counterfactual questions while providing a basis for interpreting new observations. Causal constructions require careful mathematical modelling. In the end, the data scientist attached to operations presents decision makers with the likely consequences of alternatives courses of action. By quantitatively weighing trade-offs, the data scientist helps the decision maker use his or her expertise in non-quantitative reasoning to reach the best possible decision.

Turning the quantitative part of the decision problem into mathematics requires the data scientist to be an applied mathematician. This requirement goes well beyond the usual undergraduate exposure to linear algebra and calculus. Mathematical maturity, the ability to recognize the nature of the mathematical or statistical inference problem at hand and develop models, is essential to the successful application of data science in business. Think the “physics” structure, not black boxes.

Coding

I get silly questions all the time about computer languages. Is Python better than R? Should I use Julia? Telling a computer what to do in a particular language, while technical, should not be the focus of your concerns. Learn how to write quality intelligible code; after that, which language you use is moot. Use the tool appropriate for the job (R, Python, SQL, Bash, whatever.). In our team, we have coop students who have never seen R before and by the end of their work term they are R mini-gods, building and maintaining custom R packages, Shiny websites, and R Markdown documents all within our Git repos.

Whatever data science language you choose as your primary tool, focus on building coding skills and your craft. Data cleaning and tidying is a large part of data science so at least become proficient with split/apply/combine coding structures. Communication is key, not only for clients but also for fellow data scientists. Learn how to build targeted and clean data visualizations in your final products and in your diagnostics. Think functional structure and communication, not obsessing over computer languages.

Operational context

Understanding the business that generates your datasets is paramount. All datasets have their own quirks. Those quirks tell you something about the history of how the data were collected, revealing not only messages about the data generating process itself, but also about the personalities, the biases, and working relationships of people within the business. Learning about the people part of the data will help you untangle messiness, but more importantly, it will help you identify the key individuals who know all the special intricacies of the operations. A couple of coffee conversations with the right people can immensely strengthen the final product while shortening production time-lines.

From a statistical point of view, you need to understand the context of the data – which conclusions the data can support, which ones it can’t, and which new data, if made available, would offer the best improvements to future analysis. This issue ties us back to mathematics and statistics since in the end we desire a deeper causal and counterfactual understanding of operations. Predictions are rarely enough. Think data structure and history, not raw input for algorithms.

Machine learning in finance – technical analysis for the 21th century?

I love mathematical finance and financial economics. The relationships between physics and decision sciences are deep. I especially enjoy those moments while reading a paper when I see ideas merging with other mathematical disciplines. In fact, I will be giving a talk at the Physics Department at Carleton University in Ottawa next month on data science as applied in the federal government. In one theme, I will explore the links between decision making and the Feynman-Kac Lemma – a real options approach to irreversible investment.

I recently came across a blog post which extolls the virtues of machine learning as applied to stock picking. Here, I am pessimistic of long term prospects.

So what’s going on? Back in the 1980s, time series and regression software – not to mention spreadsheets – started springing up all over the place. It suddenly became easy to create candlestick charts, calculate moving averages of convergence/divergence, and locate exotic “patterns”. And while there are funds and people who swear by technical analysis to this day, on the whole it doesn’t offer superior performance. There is no “theory” of asset pricing tied to technical analysis – it’s purely observational.

In asset allocation problems, the question comes down to a theory of asset pricing. It’s an observational fact that some types of assets have a higher expected return relative to government bonds over the long run. For example, the total US stock market enjoys about a 9% per annum expected return over US Treasuries. Some classes of stocks enjoy higher returns than others, too.

Fundamental analysis investors, including value investors, have a theory: they attribute the higher return to business opportunities, superior management, and risk. They also claim that if you’re careful, you can spot useful information before anyone else can, and, that when that information is used with theory, you can enjoy superior performance. The literature is less than sanguine on whether fundamental analysis provides any help. On the whole, most people and funds that employ it underperform the market by at least the fees they charge.

On the other hand, financial economists tell us that fundamental analysis investors are correct up to a point – business opportunities, risk, and management matter in asset valuation – but because the environment is so competitive, it’s very difficult to use that information to spot undervalued cash flows in public markets. In other words, it’s extraordinarily hard to beat a broadly diversified portfolio over the long term.

(The essential idea is that price, p(t), is related to an asset’s payoff, x(t), through a discount rate, m(t), namely: p(t) = E[m(t)x(t)]. In a simple riskless case, m(t) =1/R, where R is 1 + the interest rate (e.g., 1.05), but in general m(t) is a random variable. The decomposition of the m(t) and its theoretical construction is a fascinating topic. See John Cochrane’s Asset Pricing for a thorough treatment.)

So where does that leave machine learning? First, some arithmetic: the average actively managed dollar gets the index. That is, on average, for every actively managed dollar that outperforms, it comes at the expense of an actively managed dollar that underperforms. It’s an incontrovertible fact: active management is zero-sum relative to the index. So, if machine learning leads to sustained outperformance, gains must come from other styles of active management, and, it must also mean that the other managers don’t learn. We should expect that if some style of active management offers any consistent advantage (corrected for risk), that advantage will disappear as it gets exploited (if it existed at all). People adapt; styles change. There are lots of smart people on Wall Street. In the end, the game is really about identifying exotic beta – those sources of non-diversifiable risk which have very strange payoff structures and thus require extra compensation.

Machine learning on its own doesn’t offer a theory – the 207,684th regression coefficient in a CNN doesn’t have a meaning. The methods simply try to “learn” from the data. In that sense, applied to the stock market, machine learning seems much like technical analysis of the 1980s – patterns will be found even when there are no patterns to find. Whatever its merits, to be useful in finance, machine learning needs to connect back to some theory of asset pricing, helping to answer the question of why some classes of assets enjoy higher return than others. (New ways of finding exotic beta? Could be!) Financial machine learning is not equal to machine learning algorithms plus financial data – we need a theory.

In some circumstances theory doesn’t matter at all when it comes to making predictions. I don’t need a “theory” of cat videos to make use of machine learning for finding cats on YouTube. But, when the situation is a repeated game with intelligent players who learn from each other and who are constantly immersed in a super competitive highly remunerative environment, if you don’t have a theory of the game, it usually doesn’t end well.

Climate change: Evidence based decision making with economics

Climate change is in the news every day now. The CBC has a new series on climate change, and news sources from around the world constantly remind us about climate change issues. As we might expect, the political rhetoric has become intense.

In my previous blog post, I showed how using even relatively crude statistical models of local daily mean temperature changes can easily extract a warming signal. But to make progress, we must understand that climate change has two parts, both of which require separate but related scientific reasoning:

1) What is the level of climate change and how are humans contributing to the problem?

2) Given the scientific evidence for climate change and human contributions, what is the best course of action that humans should take?

The answer to these two questions get muddled in the news and in political discussions. The first question has answers rooted in atmospheric science, but the second question belongs to the realm of economics. Given all the problems that humanity faces, from malaria infections to poor air quality to habitat destruction, climate change is just one among many issues that competes for scarce resources. The second question is much harder to answer and I won’t offer an opinion. Instead, I would like to leave you with a question that might help center the conversation about policy and how we should act. I leave it for you to research and decide.

If humanity did nothing about climate change and the upper end of the climate warming forecasts resulted, 6 degrees Celsius by year 2100, how much smaller would the global economy be in 2100 relative to a world with no climate change at all? In other words, how does climate change affect the graph below going forward?

A cause for celebration: World GDP growth since 1960.

Become a GAMM-ateur climate scientist with mgcv

I love tennis. I play tennis incessantly. I follow it like a maniac. This January, my wife and I attended the Australian Open, and then after the tournament we played tennis every day for hours in the awesome Australian summer heat. During a water break one afternoon, I checked the weather app on my phone; the mercury reached 44 C!

The Aussie Open 2019: Rafael Nadal prepares to serve in the summer heat.

It got me to thinking about climate change and one of the gems in my library, Generalized Additive Models: An introduction with R by Professor Simon N. Wood – he is also the author of the R package mgcv (Mixed GAM Computation Vehicle with Automatic Smoothness Estimation).

First, Wood’s book on generalized additive models is a fantastic read and I highly recommend it to all data scientists – especially for data scientists in government who are helping to shape evidence based policy. In the preface the author says:

“Life is too short to spend too much time reading statistical texts. This book is of course an exception to this rule and should be read cover to cover.”

I couldn’t agree more. There are many wonderful discussions and examples in this book with breadcrumbs into really deep waters, like the theory of soap film smoothing. Pick it up if you are looking for a nice self-contained treatment of generalized additive models, smoothing, and mixed modelling. One of the examples that Wood works through is the application of generalized additive mixed modelling to daily average temperatures in Cairo Egypt (section 7.7.2 of his book). I want to expand on that discussion a bit in this post.

Sometimes we hear complaints that climate change isn’t real, that there’s just too much variation to reveal any signal. Let’s see what a bit of generalized additive modelling can do for us.

A generalized linear mixed modelling (GLMM) takes the standard form:

    \begin{align*}\boldsymbol{\mu}^b &= \mathbb{E}({\bf y}\mid{\bf b}), \\ g(\mu_i^b) &= {\bf X}_i\boldsymbol{\beta}+ {\bf Z}_i{\bf b}, \\ {\bf b} &\sim N({\bf 0}, {\boldsymbol{\psi}}_\theta), \\ y_i\mid{\bf b} &\sim \text{exponential family dist.,}\end{align}

where g is a monotonic link function, {\bf b} contains the random effects with zero expected value and with a covariance matrix {\boldsymbol{\psi}}_\theta parameterized by \theta. A generalized additive model uses this structure, but the design matrix {\bf X} is built from spline evaluations with a “wiggliness” penalty, not on the regressors directly (coefficients correspond to the coefficients of the spline). For details, see Generalized Additive Models: An Introduction with R, Second Edition.

The University of Dayton has a website with daily average temperatures from a number of different cities across the world. Let’s take a look at Melbourne, Australia – the host city of the Australian Open. The raw data has untidy bits, and in my R Markdown file I show my code and the clean up choices that I made.

The idea is to build an additive mixed model with temporal correlations. Wood’s mgcv package allows us to build rather complicated models quite easily. For details on the theory and the implementations mgcv, I encourage you to read Wood’s book. The model I’m electing to use is:

    \begin{equation*} \text{temp}_i = s_1(\text{time.of.year}_i) + s_2(\text{time}_i) + e_i,\end{equation}

where

e_i = \phi_1 e_{i-1} + \phi_2 e_{i-2}+ \epsilon_i, \epsilon_i \sim N(0,\sigma^2), s_1(\cdot) is a cyclic cubic smoothing spline that captures seasonal temperature variation on a 365 day cycle, and s_2(\cdot) is a smoothing spline that tracks a temperature trend, if any. I’m not an expert in modelling climate change, but this type of model seems reasonable – we have a seasonal component, a component that captures daily autocorrelations in temperature through an AR(2) process, and a possible trend component if it exists. To speed up the estimation, I nest the AR(2) residual component within year.

The raw temperature data for Melbourne, Australia is:

Daily mean temperature in Melbourne: 1995 – 2019.

We see a clear season pattern in the data, but there is also a lot of noise. The GAMM model will reveal the presence of a trend:

Climate change trend in Melbourne: 1995 – 2019.

We can see that Melbourne has warmed over the last two decades (by almost 2 C). Using the Dayton temperature dataset, I created a website based on the same model that shows temperature trends across about 200 different cities. Ottawa, Canada (Canada’s capital city) is included among the list of cities and we can see that the temperature trend in Ottawa is a bit wonky. We’ve had some cold winters in the last five years and while the Dayton data for Ottawa is truncated at 2014, I’m sure the winter of 2018-2019 with its hard cold spells would also show up in the trend. This is why the phenomenon is called climate change – the effect is, and will continue to be, uneven across the planet. If you like, compare different cities around the world using my website.

As a point of caution, climate change activists should temper their predictions about how exactly climate change will affect local conditions. I recall that in 2013 David Suzuki wrote about what climate change could mean for Ottawa, saying

…one of Canada’s best-loved outdoor skating venues, Ottawa’s Rideau Canal, provides an example of what to expect…with current emissions trends, the canal’s skating season could shrink from the previous average of nine weeks to 6.5 weeks by 2020, less than six weeks by 2050 and just one week by the end of the century. In fact, two winters ago, the season lasted 7.5 weeks, and last year it was down to four. The canal had yet to fully open for skating when this column was written [January 22, 2013].

The year after David Suzuki wrote this article, the Rideau Skateway enjoyed the longest consecutive days of skating in its history and nearly one of the longest seasons on record. This year (2019) has been another fantastic skating season, lasting 71 days (with a crazy cold winter). My GAMM analysis of Ottawa’s daily average temperature shows just how wild local trends can be. Unfortunately, statements like the one David Suzuki made fuels climate change skeptics. Some people will point to his bold predictions for 2020, see the actual results, and then dismiss climate change altogether. I doubt that David Suzuki intends that kind of advocacy! Climate change is complicated, not every place on the planet will see warming and certainly not evenly. And if the jet stream becomes unstable during the North American winter, climate change may bring bitterly cold winters to eastern Canada on a regular basis – all while the Arctic warms and melts. There are complicated feedback mechanisms at play; so persuading people about the phenomenon of climate change with facts instead of cavalier predictions is probably the best strategy.

Now, establishing that climate change is real and persuading people of its existence is only one issue – what to do about it is an entirely different matter. We can agree that climate change is real and mostly anthropogenic, but it does not imply that the climate lobby’s policy agenda inexorably follows. Given the expected impact of climate change on the global economy and how to think about its economic consequences in a world of scarce resources, we should seek the best evidence based policy solutions available, see for example:

Let’s use the best evidence, both from climate science and economics, as our guide for policy in an uncertain future.

Improve operations: reduce variability in the queue

I recently came across a cute problem at Public Services and Procurement Canada while working on queue performance issues. Imagine a work environment where servers experience some kind of random interruption that prevents them from continuously working on a task. We’ve all been there—you’re trying to finish important work but you get interrupted by an urgent email or phone call. How can we manage this work environment? What are the possible trade-offs? Should we try to arrange for infrequent but long interruptions or should we aim for frequent but short interruptions?

Let’s rephrase the problem generically in terms of machines. Suppose that a machine processes a job in a random run-time, T, with mean \mathbb{E}(T) = \bar t and variance \text{Var}(T) = \sigma_t^2, but with an otherwise general distribution. The machine fails with independent and identical exponentially distributed inter-arrival times. The mean time between failures is \bar f. When the machine is down from failure, it takes a random amount of time, R, to repair. The machine failure interrupts a job in progress and, once repaired, the machine continues the incomplete job from the point of the interruption. The repair time distribution has mean \mathbb{E}(R) = \bar r and variance \text{Var}(R) =\sigma_r^2 but is otherwise general. The question is: What is the mean and variance of the total processing time? The solution is a bit of fun.

The time to complete a job, \tau, is the sum of the (random) run-time, T, plus the sum of repair times (if any). That is,

    \begin{equation*}\tau = T + \sum_{i=1}^{N(T)} R_i,\end{equation}

where N(T) is the random number of failures that occur during the run-time. First, condition \tau on a run-time of t and thus,

    \begin{equation*}\tau|t = t + \sum_{i=1}^{N(t)} R_i. \end{equation}

Now, since N(t) is the number of failures by time t with exponentially distributed failures, this is a Poisson counting process:

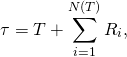
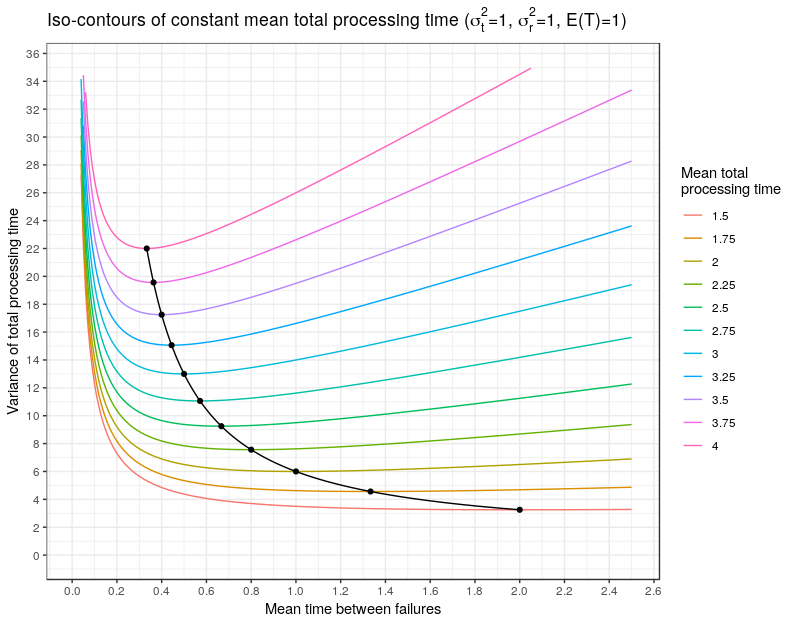
    \begin{align*} \mathbb{E}(\tau|t) &= t + \mathbb{E}\left(\sum_{i=1}^{N(t)} R_i\right) \\ &= t + \sum_{k=0}^\infty \mathbb{E}\left[\left.\sum_{i=1}^k R_i \right| N(t) = k\right]\mathbb{P}(N(t) = k) \\ &= t + \sum_{k=1}^\infty (k\bar r) \frac{(t/\bar f)^k}{k!}e^{-t/\bar f} \\ & = t + \bar r \frac{t}{\bar f}e^{-t/\bar f} \sum_{k=1}^\infty \frac{(t/\bar f)^{k-1}} {(k-1)!} \\ &= t \left(\frac{\bar f + \bar r}{\bar f}\right) \end{align}

By the law of iterated expectations, \mathbb{E}(\mathbb{E}(\tau|t)) = \mathbb{E}(\tau), and so,

    \begin{equation*} \mathbb{E}(\tau) = \mathbb{E}\left[t \left(\frac{\bar f + \bar r}{\bar f}\right)\right] = \bar t \left(\frac{\bar f + \bar r}{\bar f}\right), \end{equation}

which gives us the mean time to process a job. Notice that in the limit that \bar f\rightarrow\infty, we recover the expected result that the mean processing time is just \mathbb{E}(T) = \bar t.

To derive the variance, recall the law of total variance,

    \begin{equation*}\text{Var}(Y) = \text{Var}(\mathbb{E}(Y|X))+ \mathbb{E}(\text{Var}(Y|X))\end{equation}

From the conditional expectation calculation, we have

    \begin{equation*}\text{Var}(\mathbb{E}(\tau|t) )= \text{Var}\left[ t \left(\frac{\bar f + \bar r}{\bar f}\right)\right] = \sigma_t^2 \left(\frac{\bar f + \bar r}{\bar f}\right)^2.\end{equation}

We need \mathbb{E}(\text{Var}(\tau|t)). For fixed t, we use the Laplace transform of the sum of the random repair times, S = \sum_{i=1}^{N(t)} R_i, that is,

    \begin{align*} \mathcal{L}(u) = \mathbb{E}[\exp(uS)] &= \mathbb{E}\left[\exp\left(u\sum_{i=1}^{N(t)} R_i\right)\right] \\ &= \sum_{k=0}^\infty \left[(\mathcal{L}_r(u))^k | N(t) =k \right] \frac{(t/\bar f)^k}{k!}e^{-t/\bar f} \\ &= \exp\left(\frac{t}{\bar f}(\mathcal{L}_r(u) -1)\right), \end{align}

where \mathcal{L}_r(u) is the Laplace transform of the unspecified repair time distribution. The second moment is,

    \begin{equation*}\mathcal{L}^{\prime\prime}(0) = \left( \frac{t\mathcal{L}^\prime_r(0)}{\bar f}\right)^2 + \frac{t}{\bar f}\mathcal{L}^{\prime\prime}_r(0).\end{equation}

We have the moment and variance relationships \mathcal{L}^\prime_r(0) = \bar r and \mathcal{L}^{\prime\prime}_r(0) - (\mathcal{L}^\prime_r(0))^2 = \sigma_r^2, and thus,

    \begin{align*} \mathbb{E}[\text{Var}(\tau|T=t)] &= \mathbb{E}[\text{Var}(t + S)|T=t] \\&= \mathbb{E}[\mathcal{L}^{\prime\prime}(0) - (\mathcal{L}^\prime(0))^2] \\ &= \mathbb{E}\left[ \left(\frac{t\bar r}{\bar f}\right)^2 + \frac{t(\sigma_r^2 + \bar r^2)}{\bar f} - \left(\frac{t\bar r}{\bar f}\right)^2 \right] \\ & = \mathbb{E}\left[\frac{t(\sigma_r^2 + \bar r^2)}{\bar f}\right] = \frac{\bar t(\sigma_r^2 + \bar r^2)}{\bar f} . \end{align}

The law of total variance gives the desired result,

    \begin{align*} \text{Var}(\tau) &= \text{Var}(\mathbb{E}(\tau|t) ) + \mathbb{E}[\text{Var}(\tau|t)] \\ & = \left(\frac{\bar r + \bar f}{\bar f}\right)^2\sigma_t^2 + \left(\frac{\bar t}{\bar f}\right) \left(\bar r^2 + \sigma_r^2\right) \end{align}

Notice that the equation for the total variance makes sense in the \bar f \rightarrow \infty limit; the processing time variance becomes the run-time variance. The equation also has the expected ingredients by depending on both the run-time and repair time variance. But the equation also has a bit of a surprise, it depends on the square of the mean repair time, \bar r^2. That dependence leads to an interesting trade-off.

Imagine that we have a setup with fixed \sigma_t, \sigma_r, and \bar t, and fixed \mathbb{E}(\tau) but we are free to choose \bar f and \bar r. That is, for a given mean total processing time, we can choose between a machine that fails frequently with short repair times or we can choose a machine that fails infrequently but with long repair times. Which one would we like, and does it matter since either choice leads to the same mean total processing time? At fixed \mathbb{E}(\tau) we must have,

    \begin{equation*} \left(\frac{\bar f + \bar r}{\bar f}\right)=K,\end{equation}

for some constant K. But since the variance of the total processing time depends on \bar r, different choices of \bar f will lead to different total variance. The graph shows different iso-contours of constant mean total processing time in the total variance/mean time between failure plane. Along the black curve, we see that as the mean total processing time increases, we can minimize the variance by choosing a configuration where the machine fails often but with short repair times.

Minimizing total variance as a function of mean time between failures.

Why is this important? Well, in a queue, all else remaining equal, increasing server variance increases the expected queue length. So, in a workflow, if we have to live with interruptions, for the same mean processing time, it’s better to live with frequent short interruptions rather than infrequent long interruptions. The exact trade-offs depend on the details of the problem, but this observation is something that all government data scientists who are focused on improving operations should keep in the back of their mind.

Data science in government is really operations research

Colby Cosh had an interesting article in The National Post this week, Let’s beat our government-funded AI addiction together. In his article he refers to a Canadian Press story about the use of artificial intelligence in forest fire management. He has this to say:

“You start with your observations. What have you seen in the past decades in terms of where wildfires have occurred and how big they got? And you look for correlations with any factor that might have any impact. The question is which data really does have any correlation. That’s where the AI comes in play. It automatically figures those correlations out.”

As a reader you might be saying to yourself “Hang on: up until the part where he mentioned ‘AI’, this all just sounds like… regular scientific model-building? Didn’t statistics invent stuff like ‘correlations’ a hundred years ago or so?” And you’d be right. We are using “AI” in this instance to mean what is more accurately called “machine learning.” And even this, since it mentions “learning,” is a misleadingly grandiose term.

Cosh has a point. Not only are labels like artificial intelligence being attached to just about everything involving computation these days, but just about everyone who works with data is now calling themselves a data scientist. I would like to offer a more nuanced view, and provide a bit of insight into how data science actually works in the federal government as practiced by professional data scientists.

Broadly, data science problems fall into two areas:

1) Voluminous, diffuse, diverse, usually cheap, data with a focus on finding needles in haystacks. Raw predictive power largely determines model success. This situation is the classic Big Data data science problem and is tightly associated with the realm of artificial intelligence. The term Big Data sometimes creates confusion among the uninitiated – I’ve seen the occasional business manager assume that large data sets refer to a file that’s just a bit too large to manage with Excel. In reality, true Big Data comprises of data sets that cannot fit into memory on a single machine or be processed by a single processor. Most applications of artificial intelligence require truly huge amounts of training data along with a host of specialized techniques to process it. Examples include finding specific objects within a large collection of videos, voice recognition and translation, handwriting and facial recognition, and automatic photo tagging.

2) Small, dense, formatted, usually expensive data with a focus on revealing exploitable relationships for human decision making. Interpretability plays a large role in determining model success. Unlike the Big Data problems, relevant data almost always fit into memory on a single machine amenable to computation with a limited number of processors. These moderate-sized problems fit within the world of operations research and theoretical models of the phenomenon provide important guides. Examples include modelling queues, inventories, optimal stopping, and trade-offs between exploration and exploitation. A contextual understanding of the data and the question is paramount.

Government data science problems are almost always of the second type, or can be transformed into the second type with a bit of effort. Our data is operational in nature, expensive, dense, small (under 30 GB), rectangular, approximately well-formatted (untidy with some errors, but not overly messy) with a host of privacy and sometimes security concerns. Government decision makers seek interpretable relationships. The real world is more complicated than any mathematical model, hence the need for a decision maker in the first place. The decision maker’s experience is an essential part the process. As Andrew Ng points out in the Harvard Business Review, What Artificial Intelligence Can and Can’t Do Right Now,

“If a typical person can do a mental task with less than one second of thought, we can probably automate it using AI either now or in the near future.”

Government decision making usually does not conform to that problem type. Data science in government is really operations research by another name.

Often analysts confuse the two types of data science problems. Too often we have seen examples of the inappropriate use of black-box software. Feeding a few gigabytes of SQL rectangular data into a black-box neural net software package for making predictions in a decision making context is almost certainly misplaced effort. Is the black-box approach stronger? As Yoda told Luke, “No, no, no. Quicker, easier, more seductive.” There is no substitute for thinking about the mathematical structure of the problem and finding the right contextual question to ask of the data.

To give a more concrete example, in the past I was deeply involved with a queueing problem that the government faced. Predicting wait times, queue lengths, and arrivals, is not a black-box-plug-and-play problem. To help government decision makers better allocate scarce resources, we used queueing theory along with modern statistical inference methods. We noticed that servers across our queue came from a heterogeneous population of experience and skill, nested within teams. We estimated production using hierarchical models and Markov Chain Monte Carlo which we used to infer some aspects of our queueing models. We were not thinking about driving data into black-boxes, we were more concerned with the world of random walks, renewal theory, and continuous time Markov chains. Our modelling efforts engendered management discussions that focus on trade-offs between a reduction in server time variance, increasing average service speed, and adding to queue capacity; all of which play a role in determining the long term average queue length and all of which have their own on-the-ground operational quirks and costs. Data science, as we practice it in the civil service, moves management discussions to a higher level so that the decision maker’s unique experience and insight becomes crucial to the final decision. Raw predictive power is usually not the goal – an understanding of how to make optimal trade-offs with complex decisions is.

Data science in government is about improving decisions through a better understanding of the world. That’s mostly the application of operations research and that is how our group applies computation and mathematics to government problems.