Operations research - The Reformed Physicist

Ontario ICU arrivals and departures as a Skellam process

Figure 1: Net daily change in the Ontario ICU census with Skellam inferred rates. The red lollipop points are days of net inflow and blue lollipop points are days of net outflow. The red ribbon and blue ribbons are the inferred daily ICU arrival and departure rates from the Skellam process. Lockdown imposition and lifting dates indicated.

As Ontario enters a new lockdown, the main concern is a potential overrun of our ICU capacity. A year ago, the Ontario government announced a planned major expansion of provincial ICU capacity, but, given our current limits, it appears that either the plan never came to fruition or that the efforts woefully underestimated possible COVID-19 ICU demand. The Ontario COVID-19 data portal gives the daily ICU COVID-19 census from which we can compute daily changes. As of April 4, Ontario has 451 ICU patients associated with COVID-19. The daily changes give us the net flow but the counting does not tell us how many people actually arrived or departed each day. When we see a daily uptick of 25 people, is that 25 arrivals with no departures or is it 50 arrivals with 25 departures? Both scenarios give the same net change.

Even though the COVID-19 data shows only the net change, we can infer the arrival and departure rates using the Skellam distribution. The Skellam distribution is the difference of two Poisson distributions, $k = n_1 - n_2$ , given by the convolution with a negative sum, namely,

(1) $\begin{equation*} s(k; \mu_1,\mu_2) = \sum_{n=-\infty}^\infty\, p(k+n; \mu_1) p(n; \mu_2),\end{equation*}$

where $s(k; \mu_1, \mu_2)$ has support on $\{\ldots, -2,-1,0,1,2,\dots\}$ , and $p(k;\mu) = \frac{\mu^k}{k!}e^{-\mu}$ is the Poisson. The resulting distribution can be expressed in terms of the modified Bessel function,

(2) $\begin{equation*}s(k; \mu_1, \mu_2) = e^{-(\mu_1 + \mu_2)}\left(\frac{\mu_1}{\mu_2}\right)^{k/2} I_{|k|}(2\sqrt{\mu_1\mu_2}) .\end{equation*}$

I take the daily difference in the Ontario ICU census data and estimate the Skellam distribution over a 21 day sliding window. The Skellam parameters are the ribbons in figure 1, smoothed with cubic splines with cross validation, and superimposed on the daily net flow. The red ribbon is the arrival process and the blue ribbon is the departure process. Each lollipop point is the net change in the ICU occupation on that day. In figure 2 I show a Q-Q plot of the Pearson residuals from the Skellam model – the model is a reasonably good description of the data generating process. In my analysis I use the R packages Skellam and mgcv (for spline estimation). For clarity, I indicate the lockdown imposition and lockdown lift dates. As of early April 2021, it looks like we are approaching an average of 50 admissions to the ICU every day with an average departure of about 40.

Causation is hard to determine in regressions such as this model, but we see that after the lockdown date on December 26, 2020, the arrival rate quickly plateaued only to begin rising again near the end of the lockdown period. It appears that the lockdown this winter had the effect of tempering arrivals into the ICU. But as always with statistics, we need to be cautious about making causal statements. The arrivals in the ICU are from people who were infected at an earlier date, probably in the neighbourhood of one week earlier. Thus, we see that the arrival rate remains high from the beginning of the lockdown on December 26 through the end of December and early January. We should expect this inertia from infections that occurred near or before the imposition of the lockdown, although there is a distinct possibility that people started to change their behaviour before the lockdown date. But notice that the arrival rate begins to rise sharply almost exactly coincidental with the end of the lockdown on February 16, 2021. This observation suggests that infections were beginning to accelerate at least a week, maybe two, prior to the end of the lockdown. It appears that we would have seen a surge at some level in Ontario’s ICUs even if the lockdown had been maintained through the end of February or longer. Of course it’s quite probable that the resulting surge would have been smaller than the one we are currently witnessing, but to gain insight into such a counterfactual we need to know what caused the acceleration in infections prior to the end of the lockdown. If infections started to rise before the end of the lockdown, is it the result of the new more contagious variants? Is it lockdown fatigue? Is it spread among essential workers? Maybe it’s a combination of effects; I don’t know. Lockdown efficacy rests on that understanding.

Notice that the arrival process turned downward, or at least plateaued, about two weeks after the lockdown date of December 26, 2020, but also notice that the daily number of departures has been steadily increasing throughout the entire winter. Of course we expect that as arrivals increase, departures will eventually increase as well – everyone who enters the ICU eventually leaves. In a steady-state queue, the average departure rate will equal the average arrival rate. With time variation in the arrival process the departure rate will lag as the arrival rate waxes and wanes. It might be instructive to think about the average server load (ICU occupation) of an M/M/c queue (exponentially distributed arrival time, exponentially distributed server times, with c servers) as an approximation to the ICU dynamics. In an M/M/c queue the average number of busy servers (ICU bed occupation) is,

(3) $\begin{equation*} \bar c = \frac{\mu}{\tau}, \end{equation*}$

where $\mu$ is the arrival rate and $\tau$ is the average service rate. For example, given an arrival rate of 50 people per day and an average length of stay of 14 days in the ICU, the steady-state average number of people in the ICU would be 700 patients, provided the number of beds (servers) is larger than 700. I don’t know if the length of stay has been varying over time. It would be great to do a full time dependent competing risk survival analysis on that data, but the steady rise in the departure rate that we see over the winter might indicate that the length of stay in the ICU has also been changing with the arrival rate. I don’t know.

There are a number of ways to extend this work. The estimator is crude – instead of a naive 21 day sliding window, it could be built with a Bayesian filter. The Q-Q plot in figure 2 shows that the naive sliding window generates a good fit to the data but if we want to back-out robust estimates of the timing of the infections associated with the arrivals, it might be worth exploring filtering. Second, it is possible to promote the parameters of the Skellam process to functions of other observables such as positive test rates, lagged test rates, time, or any other appropriate regressor and then estimate the model through non-linear minimization. In fact, initially I approached the problem using a polynomial basis over time with regression coefficients, but the sliding window generates a better fit.

Where does this leave us? The precipitous drop in ICU arrivals throughout the summer of 2020 with low social distancing stringency and no lockdowns, along with the steady rise in arrivals beginning in the fall, suggest that Covid-19 will become part of the panoply of seasonal respiratory viruses that appear each year. Hopefully with the vaccines and natural exposure, future seasonal case loads will occur with muted numbers relative to our current experience. Given that the largest mitigating effect, next to vaccines, seems to be the arrival of spring and summer, lockdown or not, the warming weather accompanied by greater opportunities to be outdoors should have a positive effect. Covid-19 cases are plummeting across the southern US states like Texas and Alabama, yet cases are rising in colder northern states like New York and New Jersey. While increased herd immunity in the US from higher levels of vaccination and higher levels of natural exposure must be having an effect on reducing spread, it really does seem like Covid-19 behaves as a seasonal respiratory illness. Hopefully we can expect better days ahead, but, in the end, it is very hard to maintain a large susceptible population in the face of a highly contagious virus that has already become widespread. Perhaps we should have been looking for better public health policies all along.

Covid-19 branching model: details and calibration to data

Last month my collaborators, Jerome Levesque and David Shaw, and I built a branching process model for describing Covid-19 propagation in communities. In my previous blog post, I gave a heuristic description of how the model works. In this post, I want to expand on some of the technical aspects of the model and show how the model can be calibrated to data.

The basic idea behind the model is that an infected person creates new infections throughout her communicable period. That is, an infected person “branches” as she generates “offspring”. This model is an approximation of how a communicable disease like Covid-19 spreads. In our model, we assume that we have an infinite reservoir of susceptible people for the virus to infect. In reality, the susceptible population declines – over periods of time that are much longer than the communicable period, the recovered population pushes back on the infection process as herd immunity builds. SIR and other compartmental models capture this effect. But over the short term, and especially when an outbreak first starts, disease propagation really does look like a branching process. The nice thing about branching processes is that they are stochastic, and have lots of amazing and deep relationships that allow you to connect observations back to the underlying mechanisms of propagation in an identifiable way.

In our model, both the number of new infections and the length of the communicable period are random. Given a communicable period, we model the number of infectious generated, $Q(t)$ , as a compound Poisson process,

(1) $\begin{equation*}Q(t) = \sum_{i=1}^{N(t)} \, Y_i,\end{equation*}$

where $N(t)$ is the number of infection events that arrived up to time $t$ , and $Y_i$ is the number infected at each infection event. We model $Y_i$ with the logarithmic distribution,

(2) $\begin{equation*}\mathbb{P}(Y_i =k) = \frac{-1}{\ln(1-p)}\frac{p^k}{k}, \hspace{2em} k \in {1,2,3,\ldots}.\end{equation*}$

which has mean, $\mu = -\frac{p}{(1-p)\ln(1-p)}$ . The infection events arrive exponentially distributed in time with arrival rate $\lambda$ . The characteristic function for $Q(t)$ reads,

(3) $\begin{align*}\phi_{Q(t)}(u) &=\mathbb{E}[e^{iuQ(t)}] \\ &= \exp\left(rt\ln\left(\frac{1-p}{1-pe^{iu}}\right)\right) \\ &= \left(\frac{1-p}{1-pe^{iu}}\right)^{rt},\end{align*}$

with $\lambda = -r\ln(1-p)$ and thus $Q(t)$ follows a negative binomial process,

(4) $\begin{equation*}Q(t) \sim \mathrm{NB}(rt,p).\end{equation*}$

The negative binomial process is important here. Clinical observations suggest that Covid-19 is spread mostly by a minority of people in large quantities. Research suggests that the negative binomial distribution describes the number of infections from infected individuals. In our process, during a communicable period, $t$ , an infected individual infects $Q(t)$ people based on a draw from the negative binomial with mean $rtp/(1-p)$ . The infection events occur continuously in time according to the Poisson arrivals. However, the communicable period, $t$ , is in actuality a random variable, $T$ , which we model as a gamma process,

(5) $\begin{equation*}f_{T(t)}(x) = \frac{b^{at}}{\Gamma(at)} x^{at-1}e^{-b x},\end{equation*}$

which has a mean of $\mean{T} = at/b$ . By promoting the communicable period to a random variable, the negative binomial process changes into a Levy process with characteristic function,

(6) $\begin{align*}\mathbb{E}[e^{iuZ(t)}] &= \exp(-t\psi(-\eta(u))) \\ &= \left(1- \frac{r}{b}\ln\left(\frac{1-p}{1-pe^{iu}}\right)\right)^{-at},\end{align*}$

where $\eta(u)$ , the Levy symbol, and $\psi(s)$ , the Laplace exponent, are respectively given by,

(7) $\begin{align*}\mathbb{E}[e^{iuQ(t)}] &= \exp(t\,\eta(u)) \\\mathbb{E}[e^{-sT(t)}] &= \exp(-t\,\psi(s)), \end{align*}$

and so,

(8) $\begin{align*}\eta(u) &= r\ln\left(\frac{1-p}{1-pe^{iu}}\right), \\\psi(s) &= a\ln\left(1 + \frac{s}{b}\right).\end{align*}$

$Z(t)$ is the random number of people infected by a single infected individual over her random communicable period and is further over-dispersed relative to a pure negative binomial process, getting us closer to driving propagation through super-spreader events . The characteristic function in eq.(6) for the number of infections from a single infected person gives us the entire model. The basic reproduction number $R_0$ is,

(9) $\begin{align*}R_0 &= \left(\frac{at\lambda}{b}\right)\left(\frac{-p}{\ln(1-p)(1-p)}\right).\end{align*}$

From the characteristic function we can compute the total number of infections in the population through renewal theory. Given a random characteristic $\chi(t)$ , such as the number of infectious individuals at time $t$ , (e.g., $\chi(t) = \mathbb{I}(t \in [0,\lambda_x))$ where $\lambda_x$ is the random communicable period) the expectation of the process follows,

(10) $\begin{equation*}\mathbb{E}(n(t)) = \mathbb{E}(\chi(t)) + \int_0^t\mathbb{E}(n(t-u))\mathbb{E}(\xi(du)).\end{equation*}$

where $\xi(du)$ is the counting process (see our paper for details). When an outbreak is underway, the asymptotic behaviour for the expected number of counts is,

(11) $\begin{equation*}\mathbb{E}(n_\infty(t)) \sim \frac{e^{\alpha t}}{\alpha\beta},\end{equation*}$

where,

(12) $\begin{align*}\alpha &= \lambda\mu \left(1 - \left(\frac{b}{\alpha +b}\right)^{at}\right) \\\beta & = \frac{1}{\alpha}\left(1 - \frac{at\lambda \mu}{b}\left(\frac{b}{\alpha +b}\right)^{at+1}\right).\end{align*}$

The parameter $\alpha > 1$ is called the Malthusian parameter and it controls the exponential growth of the process. Because the renewal equation gives us eq.(11), we can build a Bayesian hierarchical model for inference with just cumulative count data. We take US county data, curated by the New York Times, to give us an estimate of the Malthusian parameter and therefore the local $R$ -effective across the United States. We use clinical data to set the parameters of the gamma distribution that controls the communicable period. We treat the counties as random effects and estimate the model using Gibbs sampling in JAGS. Our estimation model is,

(13) $\begin{align*}\log(n) &= \alpha t + \gamma + a_i t + g_i + \epsilon \nonumber \\a_i &\sim \text{N}(0,\sigma_1^2) \nonumber \\g_i & \sim \text{N}(0,\sigma_2^2) \nonumber \\\epsilon &\sim \text{N}(0,\sigma^2),\end{align*}$

where $i$ is the county label; the variance parameters use half-Cauchy priors and the fixed and random effects use normal priors. We estimate the model and generate posterior distributions for all parameters. The result for the United States using data over the summer is the figure below:

Summer 2020 geographical distribution of R-effective across the United States: 2020-07-01 to 2020-08-20.

Over the mid-summer, we see that the geographical distribution of $R_{eff}$ across the US singles out the Midwestern states and Hawaii as hot-spots while Arizona sees no county with exponential growth. We have the beginnings of a US county based app which we hope to extend to other countries around the world. Unfortunately, count data on its own does not allow us to resolve the parameters of the compound Poisson process separately.

If we have complete information, which might be possible in a small community setting, like northern communities in Canada, prisons, schools, or offices, we can build a Gibbs sampler to estimate all the model parameters from data without having to rely on the asymptotic solution of the renewal equation.

Define a complete history of an outbreak as a set of $N$ observations taking the form of a 6-tuple:

(14) $\begin{equation*}(i,j,B_{i},D_{i},m_{i},o_{i}),\end{equation*}$

where,

$i$ : index of individual, $j$ : index of parent, $B_{i}$ : time of birth, $D_{i}$ : time of death, $m_{i}$ : number of offspring birth events, $o_{i}$ : number of offspring.

With the following summary statistics:

(15) $\begin{align*}L & = \sum_{i} D_{i} - B_{i};\,\, \Lambda = \prod_{i} (D_{i} - B_{i}) \nonumber \\ M & = \sum_{i} m_{i};\,\, O = \sum_{i} o_{i} \nonumber \end{align*}$

we can build a Gibbs sampler over the models parameters as follows:

(16) $\begin{align*}p\,|\,r,L,O & \sim \text{Beta}\left(a_{0} + O,b_{0} + r L\right) \nonumber \\r\,|\,p,L,M & \sim \text{Gamma}\left(\eta_{0}+M,\rho_{0}-L\log(1-p)\right) \nonumber \\b\,|\,a,L,N & \sim \text{Gamma}\left(\gamma_{0}+aN,\delta_{0}+L\right)\nonumber \\a\,|\,b,\Lambda,N & \sim\text{GammaShape}\left(\epsilon_{0}\Lambda,\zeta_{0}+N,\theta_{0}+N\right)\end{align*}$

where $a_0, b_0, \eta_0, \rho_0, \gamma_0, \zeta_0, \epsilon_0, \theta_0$ are hyper-parameters.

Over periods of time that are comparable to the communicable window, such that increasing herd immunity effects are negligible, a pure branching process can describe the propagation of Covid-19. We have built a model that matches the features of this disease – high variance in infection counts from infected individuals with a random communicable period. We see promise in our model’s application to small population settings as an outbreak gets started.

An effective theory of Covid-19 propagation

To fight Covid-19, we need an understanding of how the virus propagates in a community. Right now, the workhorse engine in the literature and in the media are compartmental models: (S)usceptible (I)nfected (R)ecovered and its cousins. The most popular versions of these models start with a set of coupled ordinary differential equations which, when solved, generate paths for each compartment. For example, in the simple SIR model, the infection starts with a large susceptible population which diminishes as the infected population rises. The infected population eventually declines as the recovered population increases and eventually the infected population goes to zero as the outbreak ends. The differential equations govern the dynamics of each compartment, generating equations of motion for the population.

Covid-19 propagation as a gamma subordinated negative binomial branching process

SIR models work well when we are discussing large populations, when we are interested in population averages, and when the random nature of the transmission doesn’t particularly matter. The solution to the coupled set of differential equations is deterministic. But when an outbreak gets started or when we are interested in the dynamics in the small population limit, we need more than deterministic models. SIR compartmental model with its focus on averages is not enough when dealing with the very early stages of an outbreak – and it’s the early stages where we really want our mitigation strategies to be the most successful. We need a stochastic model of transmission to understand the early stages of an outbreak.

Together with my colleagues Jerome Levesque, and David Shaw, we built a branching model of Covid-19 propagation. The idea is that an infected person randomly infects other people over the course of the communicable period. That is, we model transmission by imagining that an infected person generates “offspring”, continuous in time, during the communicable period and that each “child” has the same statistical law for generate more “offspring”. The infections branch out from each infected person into a tree that makes up the infected community. So while on average an infected person will infect R0 other people (the basic reproduction number) during the communicable period, there are a range of possible outcomes. We could get lucky and an initially infected person might not spread the virus at all, or we could get unlucky and the initially infected person might become a super-spreader, all in a model with the same R0. In fact, even with R0>1, there can be a substantial probability that the outbreak will go extinct on its own, all depending on the statistical branching nature of transmission.

In some research communities, there is a tendency to use agent based models to capture the stochastic nature of an outbreak. Such models simulate the behaviour of many different individuals or “agents” in a population by assigning a complicated set of transmission rules to each person. In the quest for high fidelity, agent based models tend to have lots of parameters. While agent based approaches have merit, and they have enjoyed success in many fields, we feel that in this context these models are often too difficult to interpret, contain many layers of hidden assumptions, are extraordinarily difficult to calibrate to data while containing lots of identifiability issues, are easily susceptible to chaotic outputs, and obscure trade-off analysis for decision makers. In a decision making context we need a parsimonious model, one that gets the essentials correct and generates insight for trade-off analysis that decision makers can use. We need an effective theory of Covid-19 propagation in which we project all the complicated degrees of freedom of the real world down to a limited number of free parameters around which we can build statistical estimators.

The abstract of our paper:

We build a parsimonious Crump-Mode-Jagers continuous time branching process of Covid-19 propagation based on a negative binomial process subordinated by a gamma subordinator. By focusing on the stochastic nature of the process in small populations, our model provides decision making insight into mitigation strategies as an outbreak begins. Our model accommodates contact tracing and isolation, allowing for comparisons between different types of intervention. We emphasize a physical interpretation of the disease propagation throughout which affords analytical results for comparison to simulations. Our model provides a basis for decision makers to understand the likely trade-offs and consequences between alternative outbreak mitigation strategies particularly in office environments and confined work-spaces.

We focus on two parameters that decision makers can use to set policy: the average waiting time between infectious events from an infected individual, and the average number of people infected at an event. We fix the communicable period (distribution) from clinical data. Those two parameters go into the probabilistic model for branching the infection through the population. The decision maker can weigh trade-offs like restricting meeting sizes and interaction rates in the office while examining the extinction probabilities, growth rates, and size distributions for each choice.

You can find our paper here: https://medrxiv.org/cgi/content/short/2020.07.08.20149039v1

Covid-19 and decisions under uncertainty

Three excellent essays recently appeared in the Boston Review by Jonathan Fuller, John Ioannidis, and Marc Lipsitch on the nature of epidemiology, and the use of data in making public health decisions. Each essay makes great points, especially Professor Ioannidis’ emphasis that Covid-19 public health decisions constitute trade-offs – other people will die based on our decisions to mitigate Covid-19. But I think all of all three essays miss the essential question, which transcends Covid-19 or even public health:

What is the optimal way to make irreversible decisions under uncertainty?

The answer to this question is subtle because it involves three competing elements: time, uncertainty, and irreversibility. In a decision making process, time gives us the opportunity to learn more about the problem and remove some of the uncertainty, but it’s irreversibility that makes the problem truly difficult. Most important problems tend to have a component of irreversibility. Once we make the decision, there is no going back or it is prohibitively expensive to do so, and our opportunity to learn more about the problem is over.

Irreversibility coupled with uncertainty and time means there is value in waiting. By acting too soon, we lose the opportunity to make a better decision, and by waiting too long, we miss the opportunity altogether. Waiting and learning incurs a cost, but that cost is often more than offset by the chance to make a better and more informed decision later. The value of waiting in finance is part of option pricing and that value radically changes optimal decision making. There is an enormous amount of research on option valuation with irreversible decisions. The book Investment Under Uncertainty by Avinash Dixit and Robert Pindyck provides a wonderful introduction to the literature. When faced with an irreversible decision, the option value can be huge, even dwarfing the payoff from immediate action. At times, learning is the most valuable thing we can do. But for the option to have value, we must have time to wait. In now-or-never situations, the option loses its value completely simply because we have no opportunity to learn. The take-a-way message is this: the more irreversible the decision, the more time you have, and the more uncertainty you face, the larger the option value. The option value increases along each of these dimensions, thereby increasing the value of waiting and learning.

Covid-19 has all of these ingredients – time, uncertainty, and irreversibility. Irreversibility appears through too many deaths if we wait too long, and economic destruction requiring decades of recovery if we are too aggressive in mitigation (while opening up global financial risks). There is a ton of uncertainty surrounding Covid-19 with varying degrees of limited time windows in which to act.

Those who call for immediate and strong Covid-19 mitigation strategies recognize irreversibility – we need to save lives while accepting large economic costs – and that even though we face enormous uncertainty, the costs incurred from waiting are so high compared to immediate action that the situation is ultimately now-or-never. There is no option value. Those who call for a more cautious and nuanced approach also see the irreversibility but feel that while the costs from learning are high and time is short, the option value is rescued by the enormous uncertainty. With high uncertainty, it can be worth a lot to learn even a little. Using the lens of option valuation, read these two articles by Professor Ioannidis and Professor Lipsitch from this March and you can see that the authors are actually arguing over the competing contributions of limited time and high uncertainty to an option’s value in an irreversible environment. They disagree on the value of information given the amount of time to act.

So who’s right? In a sense, both. We are not facing one uncertain irreversible decision; we face a sequence of them. When confronted by a new serious set of problems, like a pandemic, it can be sensible to down-weight the time you have and down-weight the uncertainty (by assuming the worst) at the first stage. Both effects drive the option value to zero – you put yourself in the now-or-never condition and you act. But for the next decision, and the next one after that, with decreasing uncertainty over time, you change course, and you use information differently by recognizing the chain of decisions to come. Johan Giesecke makes a compelling argument about the need for a course change with Covid-19 by thinking along these lines.

While option valuation can help us understand the ingredients that contribute to waiting, the uncertainty must be evaluated over some probability measure, and that measure determines how we weigh consequences. There is no objectively correct answer here. How do we evaluate the expected trade-off between excess Covid-19 deaths among the elderly vs a lifetime of lost opportunities for young people? How much extra child abuse is worth the benefit of lockdowns? That weighing of the complete set of consequences is part of the totality of evidence that Professor Ioannidis emphasizes in his essay.

Not only does time, uncertainty, and irreversibility drive the option value, but so does the probability measure. How we measure consequences is a value judgment, and in a democracy that mesaure must rest with our elected officials. It’s here that I fundamentally disagree with Professor Lipsitch. In his essay, he increasingly frames the philosophy of public health action in terms of purely scientific questions. But public action, the decision to make one kind of costly trade-offs against another – and it’s always about trade-offs – is a deeply political issue. In WWII, President Truman made the decision to drop the bomb, not his generals. Science can offer the likely consequences of alternative courses of public health actions, but it is largely silent on how society should weigh them. No expert, public health official, or famous epidemiologist has special insight into our collective value judgment.

Covid-19: A case fatality rate app for US counties

I made a web app on estimating the case fatality rate (CFR) of Covid-19 across all the US counties. I use a binomial GLMM with nested random effects (state, state:county) using the R package lme4. Every time you reload the app, it fetches the most recent data and re-estimates the model.

The model “shrinks” the simple CFR estimates (dividing deaths by cases) at the county level by “learning” across the other counties within the state and by “learning” across the states themselves. The model pulls in or pushes out estimates that are too large or too small because they come from a county with a small sample size. It’s a bit like trying to estimate the true scoring rate of the NHL teams after watching only the first 10 games of the season. There will be a couple of blow-outs and shut-outs and we need to correct for those atypical results in small samples – but we should probably shrink the Leafs ability to score down to zero just to be safe 😉

The CFR data has limitations because the people who get tested are biased toward being sick, often very sick. The infection fatality rate (IFR), which is what we all really want to know, requires testing far more people. Recent evidence suggests that the IFR will end up much lower than the current CFR estimates.

The app shows the how the naive empirical estimate of the CFR compares to the shrunk estimator from the model. I also provide a forest plot to show the prediction intervals of the model estimates, including the contributions from the random effects. The prediction intervals I report are conservative. I use R’s merTools predictInterval() to include uncertainty from the residual (observation-level) variance, and the uncertainty in the grouping factors by drawing values from the conditional modes of the random effects using the conditional variance-covariance matrix. I partially corrected for the correlation between the fixed and random effect. Prediction interval estimation with mixed models is a thorny subject and short of a full Bayesian implementation, a full bootstrap of the lme4 model is required for the best estimates of the prediction interval. Unfortunately, bootstrapping my model takes too long for the purposes of my app (and so does the MCMC in a Bayesian implementation!). For details on use of the use of merTools::predictInterval(), see Prediction Intervals from merMod Objects by Jared Knowles and Carl Frederick.

Hopefully Covid-19 will pass soon. Stay safe.

Improve operations: reduce variability in the queue

I recently came across a cute problem at Public Services and Procurement Canada while working on queue performance issues. Imagine a work environment where servers experience some kind of random interruption that prevents them from continuously working on a task. We’ve all been there—you’re trying to finish important work but you get interrupted by an urgent email or phone call. How can we manage this work environment? What are the possible trade-offs? Should we try to arrange for infrequent but long interruptions or should we aim for frequent but short interruptions?

Let’s rephrase the problem generically in terms of machines. Suppose that a machine processes a job in a random run-time, $T$ , with mean $\mathbb{E}(T) = \bar t$ and variance $\text{Var}(T) = \sigma_t^2$ , but with an otherwise general distribution. The machine fails with independent and identical exponentially distributed inter-arrival times. The mean time between failures is $\bar f$ . When the machine is down from failure, it takes a random amount of time, $R$ , to repair. The machine failure interrupts a job in progress and, once repaired, the machine continues the incomplete job from the point of the interruption. The repair time distribution has mean $\mathbb{E}(R) = \bar r$ and variance $\text{Var}(R) =\sigma_r^2$ but is otherwise general. The question is: What is the mean and variance of the total processing time? The solution is a bit of fun.

The time to complete a job, $\tau$ , is the sum of the (random) run-time, $T$ , plus the sum of repair times (if any). That is,

$\begin{equation*}\tau = T + \sum_{i=1}^{N(T)} R_i,\end{equation}$

where $N(T)$ is the random number of failures that occur during the run-time. First, condition $\tau$ on a run-time of $t$ and thus,

$\begin{equation*}\tau|t = t + \sum_{i=1}^{N(t)} R_i. \end{equation}$

Now, since $N(t)$ is the number of failures by time $t$ with exponentially distributed failures, this is a Poisson counting process:

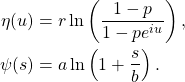
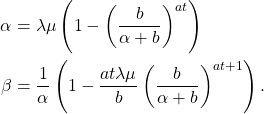
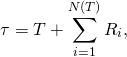
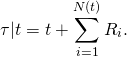
$\begin{align*} \mathbb{E}(\tau|t) &= t + \mathbb{E}\left(\sum_{i=1}^{N(t)} R_i\right) \\ &= t + \sum_{k=0}^\infty \mathbb{E}\left[\left.\sum_{i=1}^k R_i \right| N(t) = k\right]\mathbb{P}(N(t) = k) \\ &= t + \sum_{k=1}^\infty (k\bar r) \frac{(t/\bar f)^k}{k!}e^{-t/\bar f} \\ & = t + \bar r \frac{t}{\bar f}e^{-t/\bar f} \sum_{k=1}^\infty \frac{(t/\bar f)^{k-1}} {(k-1)!} \\ &= t \left(\frac{\bar f + \bar r}{\bar f}\right) \end{align}$

By the law of iterated expectations, $\mathbb{E}(\mathbb{E}(\tau|t)) = \mathbb{E}(\tau)$ , and so,

$\begin{equation*} \mathbb{E}(\tau) = \mathbb{E}\left[t \left(\frac{\bar f + \bar r}{\bar f}\right)\right] = \bar t \left(\frac{\bar f + \bar r}{\bar f}\right), \end{equation}$

which gives us the mean time to process a job. Notice that in the limit that $\bar f\rightarrow\infty$ , we recover the expected result that the mean processing time is just $\mathbb{E}(T) = \bar t$ .

To derive the variance, recall the law of total variance,

$\begin{equation*}\text{Var}(Y) = \text{Var}(\mathbb{E}(Y|X))+ \mathbb{E}(\text{Var}(Y|X))\end{equation}$

From the conditional expectation calculation, we have

$\begin{equation*}\text{Var}(\mathbb{E}(\tau|t) )= \text{Var}\left[ t \left(\frac{\bar f + \bar r}{\bar f}\right)\right] = \sigma_t^2 \left(\frac{\bar f + \bar r}{\bar f}\right)^2.\end{equation}$

We need $\mathbb{E}(\text{Var}(\tau|t))$ . For fixed $t$ , we use the Laplace transform of the sum of the random repair times, $S = \sum_{i=1}^{N(t)} R_i$ , that is,

$\begin{align*} \mathcal{L}(u) = \mathbb{E}[\exp(uS)] &= \mathbb{E}\left[\exp\left(u\sum_{i=1}^{N(t)} R_i\right)\right] \\ &= \sum_{k=0}^\infty \left[(\mathcal{L}_r(u))^k | N(t) =k \right] \frac{(t/\bar f)^k}{k!}e^{-t/\bar f} \\ &= \exp\left(\frac{t}{\bar f}(\mathcal{L}_r(u) -1)\right), \end{align}$

where $\mathcal{L}_r(u)$ is the Laplace transform of the unspecified repair time distribution. The second moment is,

$\begin{equation*}\mathcal{L}^{\prime\prime}(0) = \left( \frac{t\mathcal{L}^\prime_r(0)}{\bar f}\right)^2 + \frac{t}{\bar f}\mathcal{L}^{\prime\prime}_r(0).\end{equation}$

We have the moment and variance relationships $\mathcal{L}^\prime_r(0) = \bar r$ and $\mathcal{L}^{\prime\prime}_r(0) - (\mathcal{L}^\prime_r(0))^2 = \sigma_r^2$ , and thus,

$\begin{align*} \mathbb{E}[\text{Var}(\tau|T=t)] &= \mathbb{E}[\text{Var}(t + S)|T=t] \\&= \mathbb{E}[\mathcal{L}^{\prime\prime}(0) - (\mathcal{L}^\prime(0))^2] \\ &= \mathbb{E}\left[ \left(\frac{t\bar r}{\bar f}\right)^2 + \frac{t(\sigma_r^2 + \bar r^2)}{\bar f} - \left(\frac{t\bar r}{\bar f}\right)^2 \right] \\ & = \mathbb{E}\left[\frac{t(\sigma_r^2 + \bar r^2)}{\bar f}\right] = \frac{\bar t(\sigma_r^2 + \bar r^2)}{\bar f} . \end{align}$

The law of total variance gives the desired result,

$\begin{align*} \text{Var}(\tau) &= \text{Var}(\mathbb{E}(\tau|t) ) + \mathbb{E}[\text{Var}(\tau|t)] \\ & = \left(\frac{\bar r + \bar f}{\bar f}\right)^2\sigma_t^2 + \left(\frac{\bar t}{\bar f}\right) \left(\bar r^2 + \sigma_r^2\right) \end{align}$

Notice that the equation for the total variance makes sense in the $\bar f \rightarrow \infty$ limit; the processing time variance becomes the run-time variance. The equation also has the expected ingredients by depending on both the run-time and repair time variance. But the equation also has a bit of a surprise, it depends on the square of the mean repair time, $\bar r^2$ . That dependence leads to an interesting trade-off.

Imagine that we have a setup with fixed $\sigma_t$ , $\sigma_r$ , and $\bar t$ , and fixed $\mathbb{E}(\tau)$ but we are free to choose $\bar f$ and $\bar r$ . That is, for a given mean total processing time, we can choose between a machine that fails frequently with short repair times or we can choose a machine that fails infrequently but with long repair times. Which one would we like, and does it matter since either choice leads to the same mean total processing time? At fixed $\mathbb{E}(\tau)$ we must have,

$\begin{equation*} \left(\frac{\bar f + \bar r}{\bar f}\right)=K,\end{equation}$

for some constant $K$ . But since the variance of the total processing time depends on $\bar r$ , different choices of $\bar f$ will lead to different total variance. The graph shows different iso-contours of constant mean total processing time in the total variance/mean time between failure plane. Along the black curve, we see that as the mean total processing time increases, we can minimize the variance by choosing a configuration where the machine fails often but with short repair times.

Minimizing total variance as a function of mean time between failures.

Why is this important? Well, in a queue, all else remaining equal, increasing server variance increases the expected queue length. So, in a workflow, if we have to live with interruptions, for the same mean processing time, it’s better to live with frequent short interruptions rather than infrequent long interruptions. The exact trade-offs depend on the details of the problem, but this observation is something that all government data scientists who are focused on improving operations should keep in the back of their mind.