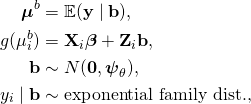Category: Computation

Estimating the Covid-19 case fatality rate using GLMM

As we are all dealing with self-isolation and social distancing in our fight against Covid-19, I thought that I would apply some quick-and-dirty mixed effects modelling with the Covid-19 case fatality rate (CFR) data.

The Centre for Evidence Based Medicine (CEBM), Nuffield Department of Primary Care Health Centre, University of Oxford (not far from my old stomping grounds on Keble Road) has put together a website that tracks the Covid-19 CFR around the world. They build an estimator using a fixed-effect inverse-variance weighting scheme, a popular method in meta-analysis, reporting the CFR by region as a percentage along with 95% confidence intervals in a forest plot. The overall estimate is suppressed due to heterogeneity. In their analysis, they drop countries with fewer than four deaths recorded to date.

I would like to take a different approach with this data by using a binomial generalized mixed model (GLMM). My model has similar features to CEBM’s approach, but I do not drop any data – regions which have observed cases but no deaths is informative and I wish to use all the data in the CFR estimation. Like CEBM, I scrape https://www.worldometers.info/coronavirus/ for the Covid-19 case data.

In one of my previous blog posts I discuss the details of GLMM. GLMM is a partial-pooling method with group data which avoids the two extreme modelling approaches of pooling all the data together for a single regression or running separate regressions for each group. Mixed modelling shares information between groups, tempering extremes and lifting those groups which have little data. I use the R package lme4, but this work can be equally done in a full Bayesian setup with Markov Chain Monte Carlo. You can see a nice illustration of “shrinkage” in mixed effects models at this site.

In my Covid-19 CFR analysis, the design matrix, X, consists of only an intercept term, the random effects, b, have an entry for each region, and the link, g(), is the logit function. My observations consist of one row per case in each region with 1 indicating the observation of death, otherwise 0. For example, at the time of writing this post, Canada has recorded 7,474 cases with 92 deaths and so my resulting observation table for Canada consists of 7,474 rows with 92 ones and 7,382 zeros. The global dataset expands to nearly 800,000 entries (one for each case). If a country or region has not recorded a death, the table for that region consists of only zeros. The GLMM captures heterogeneity through the random effects and there is no need to remove zero or low count data. The GLMM “shrinks” estimates via partial-pooling.

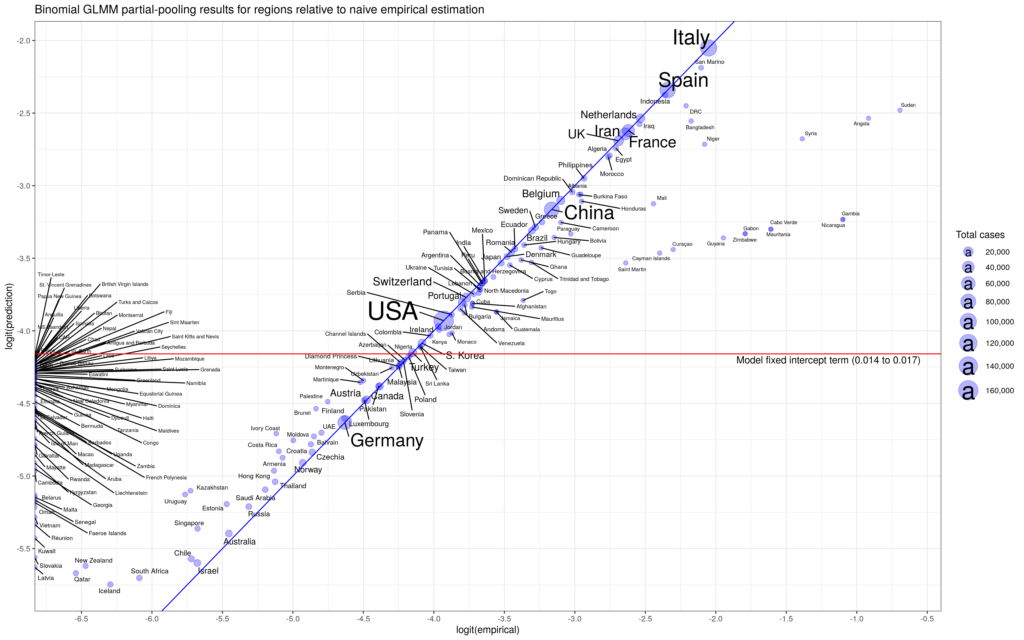
Below are my results. First, we see that the fixed effect gives a global CFR of (1.4% to 1.7%) 95% CI. This CFR is the base rate that every region sees but with its random effect that sits on top. The random effect has expectation zero, so the base CFR is the value we would use for a new region that we have not seen before and has no data yet (zero cases). Notice that, we will have a non-zero CFR for regions that have yet to observe a death over many cases – the result of partial pooling.

In the second graph we see the effect of “shrinkage” on the data. The central value for the CFR from separate regressions for each region is the x-axis (labelled empirical) while the predicted value from the GLMM is on the y-axis. Estimates that sit on the 45-degree share the same value (which we expect for regions with lots of data, less “shrinkage”). We see that regions with little data – including the group on the far left – are lifted.

I like the GLMM approach to the Covid-19 CFR data because there is so much heterogeneity between regions. I don’t know the source of that heterogeneity. Demographics is one possible explanation, but I would be interested in learning more about how each country records Covid-19 cases. Different data collection standards can also be a source of large heterogeneity.

I welcome any critiques or questions on this post. I will be making a Shiny app that updates this analysis daily and I will provide my source code.

CFR by region from a binomial GLMM. Covid-19 data taken on March 30, 2020
Regression by region vs partial-pooling. Covid-19 data taken on March 30, 2020

Become a GAMM-ateur climate scientist with mgcv

I love tennis. I play tennis incessantly. I follow it like a maniac. This January, my wife and I attended the Australian Open, and then after the tournament we played tennis every day for hours in the awesome Australian summer heat. During a water break one afternoon, I checked the weather app on my phone; the mercury reached 44 C!

The Aussie Open 2019: Rafael Nadal prepares to serve in the summer heat.

It got me to thinking about climate change and one of the gems in my library, Generalized Additive Models: An introduction with R by Professor Simon N. Wood – he is also the author of the R package mgcv (Mixed GAM Computation Vehicle with Automatic Smoothness Estimation).

First, Wood’s book on generalized additive models is a fantastic read and I highly recommend it to all data scientists – especially for data scientists in government who are helping to shape evidence based policy. In the preface the author says:

“Life is too short to spend too much time reading statistical texts. This book is of course an exception to this rule and should be read cover to cover.”

I couldn’t agree more. There are many wonderful discussions and examples in this book with breadcrumbs into really deep waters, like the theory of soap film smoothing. Pick it up if you are looking for a nice self-contained treatment of generalized additive models, smoothing, and mixed modelling. One of the examples that Wood works through is the application of generalized additive mixed modelling to daily average temperatures in Cairo Egypt (section 7.7.2 of his book). I want to expand on that discussion a bit in this post.

Sometimes we hear complaints that climate change isn’t real, that there’s just too much variation to reveal any signal. Let’s see what a bit of generalized additive modelling can do for us.

A generalized linear mixed modelling (GLMM) takes the standard form:

    \begin{align*}\boldsymbol{\mu}^b &= \mathbb{E}({\bf y}\mid{\bf b}), \\ g(\mu_i^b) &= {\bf X}_i\boldsymbol{\beta}+ {\bf Z}_i{\bf b}, \\ {\bf b} &\sim N({\bf 0}, {\boldsymbol{\psi}}_\theta), \\ y_i\mid{\bf b} &\sim \text{exponential family dist.,}\end{align}

where g is a monotonic link function, {\bf b} contains the random effects with zero expected value and with a covariance matrix {\boldsymbol{\psi}}_\theta parameterized by \theta. A generalized additive model uses this structure, but the design matrix {\bf X} is built from spline evaluations with a “wiggliness” penalty, not on the regressors directly (coefficients correspond to the coefficients of the spline). For details, see Generalized Additive Models: An Introduction with R, Second Edition.

The University of Dayton has a website with daily average temperatures from a number of different cities across the world. Let’s take a look at Melbourne, Australia – the host city of the Australian Open. The raw data has untidy bits, and in my R Markdown file I show my code and the clean up choices that I made.

The idea is to build an additive mixed model with temporal correlations. Wood’s mgcv package allows us to build rather complicated models quite easily. For details on the theory and the implementations mgcv, I encourage you to read Wood’s book. The model I’m electing to use is:

    \begin{equation*} \text{temp}_i = s_1(\text{time.of.year}_i) + s_2(\text{time}_i) + e_i,\end{equation}

where

e_i = \phi_1 e_{i-1} + \phi_2 e_{i-2}+ \epsilon_i, \epsilon_i \sim N(0,\sigma^2), s_1(\cdot) is a cyclic cubic smoothing spline that captures seasonal temperature variation on a 365 day cycle, and s_2(\cdot) is a smoothing spline that tracks a temperature trend, if any. I’m not an expert in modelling climate change, but this type of model seems reasonable – we have a seasonal component, a component that captures daily autocorrelations in temperature through an AR(2) process, and a possible trend component if it exists. To speed up the estimation, I nest the AR(2) residual component within year.

The raw temperature data for Melbourne, Australia is:

Daily mean temperature in Melbourne: 1995 – 2019.

We see a clear season pattern in the data, but there is also a lot of noise. The GAMM model will reveal the presence of a trend:

Climate change trend in Melbourne: 1995 – 2019.

We can see that Melbourne has warmed over the last two decades (by almost 2 C). Using the Dayton temperature dataset, I created a website based on the same model that shows temperature trends across about 200 different cities. Ottawa, Canada (Canada’s capital city) is included among the list of cities and we can see that the temperature trend in Ottawa is a bit wonky. We’ve had some cold winters in the last five years and while the Dayton data for Ottawa is truncated at 2014, I’m sure the winter of 2018-2019 with its hard cold spells would also show up in the trend. This is why the phenomenon is called climate change – the effect is, and will continue to be, uneven across the planet. If you like, compare different cities around the world using my website.

As a point of caution, climate change activists should temper their predictions about how exactly climate change will affect local conditions. I recall that in 2013 David Suzuki wrote about what climate change could mean for Ottawa, saying

…one of Canada’s best-loved outdoor skating venues, Ottawa’s Rideau Canal, provides an example of what to expect…with current emissions trends, the canal’s skating season could shrink from the previous average of nine weeks to 6.5 weeks by 2020, less than six weeks by 2050 and just one week by the end of the century. In fact, two winters ago, the season lasted 7.5 weeks, and last year it was down to four. The canal had yet to fully open for skating when this column was written [January 22, 2013].

The year after David Suzuki wrote this article, the Rideau Skateway enjoyed the longest consecutive days of skating in its history and nearly one of the longest seasons on record. This year (2019) has been another fantastic skating season, lasting 71 days (with a crazy cold winter). My GAMM analysis of Ottawa’s daily average temperature shows just how wild local trends can be. Unfortunately, statements like the one David Suzuki made fuels climate change skeptics. Some people will point to his bold predictions for 2020, see the actual results, and then dismiss climate change altogether. I doubt that David Suzuki intends that kind of advocacy! Climate change is complicated, not every place on the planet will see warming and certainly not evenly. And if the jet stream becomes unstable during the North American winter, climate change may bring bitterly cold winters to eastern Canada on a regular basis – all while the Arctic warms and melts. There are complicated feedback mechanisms at play; so persuading people about the phenomenon of climate change with facts instead of cavalier predictions is probably the best strategy.

Now, establishing that climate change is real and persuading people of its existence is only one issue – what to do about it is an entirely different matter. We can agree that climate change is real and mostly anthropogenic, but it does not imply that the climate lobby’s policy agenda inexorably follows. Given the expected impact of climate change on the global economy and how to think about its economic consequences in a world of scarce resources, we should seek the best evidence based policy solutions available, see for example:

Let’s use the best evidence, both from climate science and economics, as our guide for policy in an uncertain future.